This article is an excerpt from our “An In-Depth Review of Fault Tree Analysis Calculation Methods” white paper.
Fault Tree Analysis Calculation Methods
Fault Tree Analysis (FTA) is a widely used, valuable technique for assessing the possible causes of failure for a system. Using a top-down approach, FTA starts with a failure and then examines how it may be caused through the use of logic gates and lower-level events. By then attributing failure models to the various identified events, numerous helpful metrics regarding the top-level failure can be calculated. One of the most important of these results is the probability that the failure occurs, or the unavailability.
There are several methods utilized to compute unavailability in Fault Tree Analysis. These methods each have their own strengths and particular use cases where they are most advantageous. Therefore, when performing FTA, it is helpful to have an understanding of the various fault tree calculation methods in order to obtain the best results for your needs.
The white paper details the methodology behind the following fault tree calculation methods and provides examples of their usage:
- Exact
- Cut Set Summation
- Cross Product
- Esary Proschan
- Simulation

Underlying Probability Theory
The white paper provides details on the various probability terms and theory used to evaluate fault trees, such as:
Event: A probabilistic event is a set of possible outcomes in a random process. This is not the same as an event as used in Fault Tree Analysis, which is an occurrence or incident that leads to failure. In this theory section of this paper, the term event will always refer to a probabilistic event unless we are specifically talking about the structure of a fault tree. Outside of this theory section, the use of the term event will only refer to an event as used in fault trees.
Probability: The probability of an event A, written as P(A), is a value ranging from 0 to 1 that represents the likelihood of event A occurring. For practical purposes, probability can be interchanged with percent chance, so if P(A)=0.5, we can say that event A has a 50% chance of occurring.
Independence: Two events are independent if the occurrence of one does not affect the probability of the other. A set of more than two events is mutually independent if the probability of an event is unaffected by the occurrence of any combination of the other events in that set.
Intersection: The intersection of two events is the case where both events occur simultaneously.
For an arbitrary collection of events {A1, A2,…,An}, if all of the events are mutually independent, then the probability of the intersection equals the product of the individual probabilities:
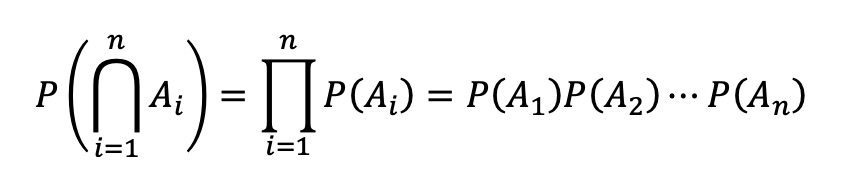
In application to FTA, the probability (or unavailability) of an AND gate in a fault tree is calculated by finding the probability for the intersection of all the direct children of that gate.
Additionally, the white paper will cover additional important theory, such as:
- Union
- Complement
- De Morgan’s Law
- Conditional Probability
- Disjoint Events
- Collectively Exhaustive Events
- Law of Total Probability

Fault Tree Exact Calculation Method
The Exact calculation method starts from the bottom of a fault tree with the events and then progresses up the tree by calculating the probabilities of the intermediate-level gates until the top gate is reached. With the Exact method, all of the gates can be calculated through the use of union, intersection, and complement.
The calculations are done assuming independence, which means that extra work is required when repeated events are present. In order to evaluate trees with repeated events, the fault tree is calculated for each combination in which the repeated events occur. For example, if there are two unique repeated events, A and B, the tree is calculated for each of these four scenarios: A and B do not occur, A occurs and B does not, A does not occur and B occurs, and both A and B occur.
With the repeated events in a known state, cases that prevent the use of independence are removed. Because exactly one repeated event combination always occurs, these combinations form a disjoint and collectively exhaustive set, so the law of total probability applies.
Because this method provides the exact results, it is the best one to use whenever possible. However, some very large and complex trees are unable to be analyzed using the Exact method. This usually happens when there are many repeated events, due to the fact that the number of calculations increases exponentially with the number of repeats.
Learn More
The white paper also explains additional Fault Tree calculation methods including Cut Set Approximations methods—Cut Set Summation, Cross Product, and Esary Proschan—as well as Simulation.
Lastly, the paper provides clear, illustrative examples using all the calculation methods for a comprehensive understanding of their strengths and particular advantageous use cases.
Download the full white paper here. To learn more about Relyence Fault Tree, feel free to contact us or schedule a personalized demonstration webinar. Or you are welcome to give us a free trial run today!





